|

Return to Unit Menu | Java Main Page |
MathBits.com |
Terms
of Use
Change a number from
any base
back to base 10:
|

|
The
computer is representing a number from the keyboard by a pattern of
ON and OFF signals represented by 1011. What number was typed
at the keyboard to produce this pattern? |
|
Let's
see how we can quickly convert numbers back to base 10 so that they
will have more meaning to us humans. |
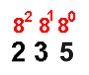
Example 1:
Convert
2358 into base 10.
|
|
The Process:
Above each of the digits in your number, list the power of the base
that the digit represents. See the example on the left.
It is now a simple process of multiplication and addition to
determine your base 10 number. In this example you have
5 x 80
= 5
3 x 81 = 24
2 x 82 = 128 |
Now simply add these values together.
5 + 24 + 128 = 157
Answer: 2358 = 15710 |
**Remember:
any number to the zero power equals one. |
Example 2:
Let's do the problem at the top of this lesson.
Convert 10112
to base 10.
|
The process is the same as in example 1.
1 x 20
= 1
1 x 21 = 2
0 x 22 = 0
1 x 23 = 8 |
1 + 2 + 0 + 8
= 11
Answer: 10112 = 1110 |
|
Example 3:
Convert 1C416 to base 10.
|
4 x 160 =
4
C x 161 = 12 x 161 = 192
1 x 162 = 256 |
4 + 192 + 256 = 452
Answer: 1C416
= 45210 |

Return to Unit Menu | Java Main Page |
MathBits.com |
Terms
of Use
|