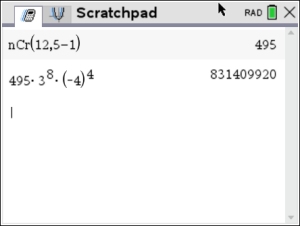
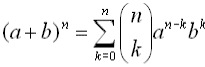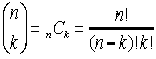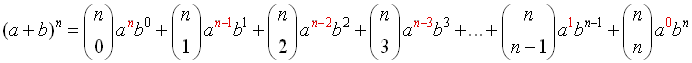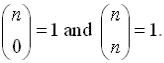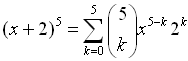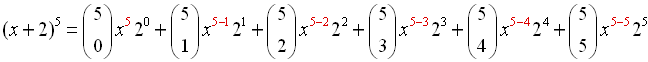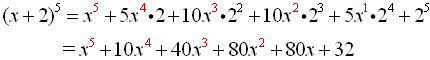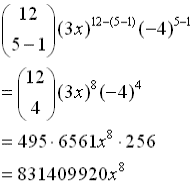Table of Contents MathBits.com Terms of Use TI-84+ Web Site

Binomial Theorem
 

Binomial Theorem
(or Binomial Expansion Theorem)
 b1

Most of the syntax used in this theorem should look familiar. The b2notation is just another way of writing a combination such as n C k  (read "n choose k").
 b3

The Binomial Theorem can also be written in its expanded form as:

b4
Remember that b6 and that b7
Note: n = the power of the expansion,    k = the number of terms in the expansion, or (n + 1)
Example 1:    Expand  b8.
Let a = x, b = 2, n = 5 and substitute.
(Do not substitute a value for k.)

 b9

   b10

Expand the Sigma listing:

b11

Now, use the calculator to quickly find the combinations b2 to simplify this equation.

This example will work on the Scatchpad.

KEYSTROKES: 

• will open the Scratchpad.

• #5 Probability, #3 Combinations

•

You can enter the 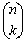b2values one at a time, such as nCr(5,0) and then nCr(5,1) and so on, for all values. Remember:  Enter the top value of the combination FIRST. 

Entering the combinations in this individual manner can be a bit tedious since we need to go back to the and start over each time.

You can enter a "list" of all of the k values in one entry such as   nCr (5,{0, 1, 2, 3, 4, 5})
where all of the values will appear at once in a set of French curly braces (to denote "list").

Remember: to get French curly braces { }, hit and the RIGHT side of parentheses keys, which is the

On the screen, you will now see a "list" of the combination values (in order) to be used in calculating the coefficients for the 6 terms in the binomial expansion for this problem. Nice!!

 

When using this quick and easy method, just be sure that the number of integers in the list is one more than the value of the power, n.

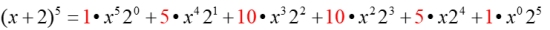
Simplifying the equation we get our final answer:

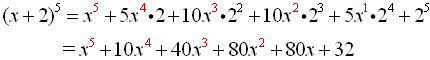
b13

 


Finding a Particular Term in a Binomial Expansion 

No one wants to work out the entire binomial expansion to find only one of the terms.
Thankfully, there is a shortcut formula:

The r th term of the expansion of   (a + b)n   is:

Example 2:    Find the 5th term of  b27.
Let r = 5, a = (3x), b = (-4), and n = 12.
Now, substitute. 

 

  
   b18 
Substitute into the formula:
     b19

Answer:
The 5th term is 831409920x8

Grab your calculator.

Use the calculator to evaluate the combination to get 495.
       
Then use the calculator to determine the coefficient of x8. Combine all of the possible numeric multiplications to get 831408820.