|
Linear Regression
A linear regression is also know as the
"line of best fit".
Side
note: Although commonly used when
dealing with "sets" of data, the linear regression can
also be used to simply find the equation of the line
between two points.
Example: Find the equation of the line passing through (-1, 1)
and (-4,7).
Entering the information as shown in the screens below, we arrive at the equation of the line:
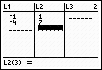   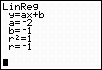 |
The equation is y = -2x
-1.
The correlation coefficient is -1
since both point are "on" the line and the line
slopes negatively. |
|
Linear Regression Model Example
Let's examine an example of the linear
regression as it pertains to a "set" of data.
|
Data:
Is there a relationship between Math
SAT scores and the number of hours spent studying for the
test? A study was conducted involving 20 students as
they prepared for and took the Math section of the SAT
Examination.
| Task: |
a.) |
Determine a linear
regression model equation to represent this data. |
| |
b.) |
Graph the new
equation. |
| |
c.) |
Decide whether the
new equation is a "good fit" to represent this data. |
| |
d.) |
Interpolate data:
If a student studied for 15 hours, based upon this study, what would be
the expected Math SAT score? |
|
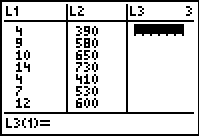
Hours Spent
Studying |
Math SAT Score |
4 |
390 |
9 |
580 |
10 |
650 |
14 |
730 |
4 |
410 |
7 |
530 |
12 |
600 |
22 |
790 |
1 |
350 |
3 |
400 |
8 |
590 |
11 |
640 |
5 |
450 |
6 |
520 |
10 |
690 |
11 |
690 |
16 |
770 |
13 |
700 |
13 |
730 |
10 |
640 |
|
| |
e.) |
Interpolate data:
If a student obtained a Math SAT score of 720, based
upon this
study, how many hours did the student most likely spend
studying? |
| |
f.) |
Extrapolate data: If a student spent 100 hours
studying, what would be the
expected Math SAT score? Discuss this answer. |
| |
Any
answers in relation to this problem are to be
rounded to the nearest tenth.
If
rounding is not indicated in a problem, leave the
full calculator entries as answers. |
|
Step 1.
Enter the data into the lists.
For basic entry of data, see Basic
Commands. |
|
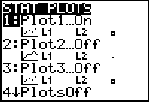
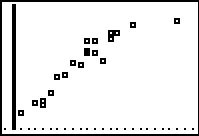
Step 2.
Create a scatter plot of the data.
Go to STATPLOT (2nd Y=)
and choose the first plot. Turn the plot
ON, set the icon to Scatter
Plot (the first one), set Xlist
to L1 and Ylist to
L2 (assuming that is where
you stored the data), and select a Mark of your choice.
  |
|
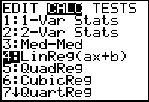
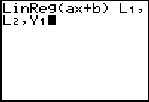
Step 3.
Choose Linear Regression Model.
Press STAT, arrow right to
CALC, and arrow down to
4: LinReg (ax+b). Hit
ENTER. When
LinReg appears on the home
screen, type the parameters L1,
L2, Y1. The Y1
will put the equation into Y=
for you.
(Y1 comes from VARS → YVARS, #Function, Y1)
|

The linear regression equation is
y = 25.3x + 353.2
(answer to part a)
|
Step 4.
Graph the Linear Regression Equation from
Y1.
ZOOM #9 ZoomStat to see
the graph. |
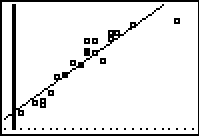
(answer to part b)
|
Step 5.
Is this model a "good fit"?
The correlation coefficient, r, is .9336055153
which places the correlation into the
"strong" category. (0.8 or greater is a "strong"
correlation)
The coefficient of determination, r
2, is .8716192582 which means
that 87% of the total variation in y can be
explained by the relationship between x and y.
The other 13% remains unexplained.
Yes, it is a "good fit". (answer
to part c) |
 |
Step 6.
Interpolate:
(within the data set)
If a student studied for 15 hours, based
upon this study, what would be the expected Math SAT
score?
From the graph screen, hit TRACE,
arrow up to obtain the linear equation at the top of the
screen, type 15, hit
ENTER, and the answer will
appear at the bottom of the screen.
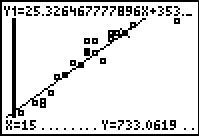
(answer to part
d --
Math SAT score of 733.1) |
Step 7.
Interpolate: (within the data set)
If a
student obtained a Math SAT score of 720, based upon
this study, how many hours did the student most likely
spend studying?
Go to TBLSET (above
WINDOW) and set the
TblStart to 13 (since 13 hours gives a score of 700).
Set the delta Tbl to a decimal setting of your choice. Go to
TABLE (above
GRAPH) and arrow up or down
to find your desired score of 720, in the Y1 column.
; 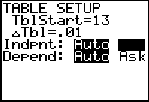

(answer to part e -- approx. 14.5 hours) |
Step 8. Extrapolate
data: (beyond the data set)
If a student spent 100 hours studying, what
would be the expected Math SAT score?
Discuss this answer.
|
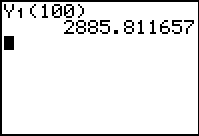 |
With your
linear equation in Y1,
go to the home screen and type
Y1(100).
Press ENTER.
Our equation shows that if a student studies
100 hours, he/she should score 2885.8 on the Math
section of the SAT examination. The only
problem with this answer is that the highest
score that can be obtained is 800. So why
is this score so outrageous? ANSWER:
When you extrapolate data, the further you move
away from the data set, the less accurate your
information becomes. In this problem, the
largest number of hours in the data set was 22
hours, but the extrapolation tried to jump to 100
hours.
(answer to part f) |
|
|


![]()