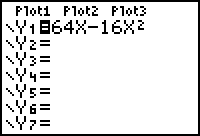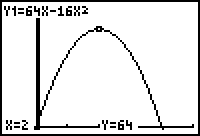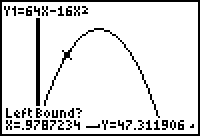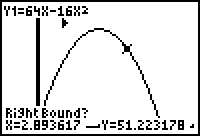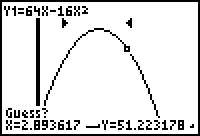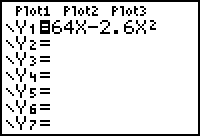|
Activity:
To determine and examine the path taken by a bottle cap projectile on the
earth and on the moon.
Mathematical
Skills: grade
level 9-12, graphing
and solving quadratic equations, graph interpretation, using a graphing
utility (a TI-84+ graphing calculator was used here)
Materials:
graph paper, graphing calculator
Directions:
| Earth: |
On Earth, it is possible to shoot a bottle cap 64 feet straight up into
the air with a rubber band. In
t
seconds after firing, the bottle cap is
s(t)
= 64t - 16t2
feet above your hand.
| a.) |
Draw a graph that simulates
the position of the bottle cap on earth. |
|
b.) |
How long does it take the
bottle cap to reach its maximum height? |
|
c.) |
What is the maximum height
reached by the bottle cap? |
|
|
|
|
| Moon: |
On the moon, the same force will send
the bottle cap to a height of
s(t) = 64t - 2.6t2
feet in t seconds.
| a.) |
Draw a graph that simulates
the position of the bottle cap on the moon. |
| b.) |
Approximately, how long does
it take the bottle cap to reach its maximum
height? |
| c.) |
Estimate the maximum height
reached by the bottle cap to the nearest tenth of
a foot? |
|
For the teacher:
While this problem can be
solved with paper and pencil, the use of the graphing calculator will
offer students a visual interpretation of the problem and reinforce
graphing concepts.
One possible solution using
the TI-84+ graphing calculator:
|
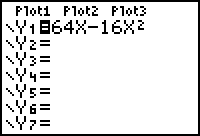
Type the equation
into Y1.
Discuss why using the variable "x" will yield the
same result as using the variable "t".
|
|

Determine a window by trial and error or
by a prior algebraic solution obtained by setting the function
equal to zero and solving for t.
|
|
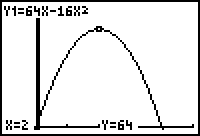
Hit graph. Is this value seen
in the window after hitting
"trace"
the actual maximum value?
|
|

Find the actual maximum value using the
calculator's maximum function.
(found under "calc" above the "trace"
key)
|
|
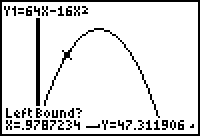
The maximum function will ask for
a left bound. Move the "spider"
(cursor) to the left of where you
imagine the maximum to be located.
Hit enter.
|
|
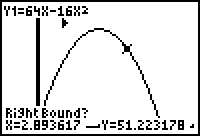
Move the "spider" to the right
of where you imagine the maximum to be located.
Hit enter.
|
|
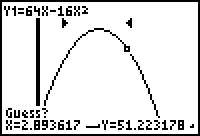
When asked to "guess", just
press "enter." Notice the pointers
surrounding the area where the
maximum will occur.
|
|
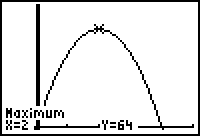
Hitting "enter" will yield
the
x and y values of the maximum.
|
|
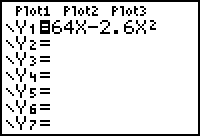
Repeat the process for
the
second equation.
|
|
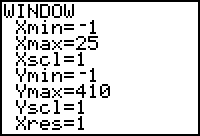
Possible window. Students should predict if the time span will increase and discuss why or why not.
|
|
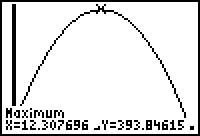
Answer.
|
|
Students should discuss
why the same force created different paths for the bottle cap on
the earth and on the moon. This is a good opportunity to engage
in "writing in the mathematics classroom." |
|