Directions: Questions #1 - 5 pertain to the derivative graph f ' (x) shown below. You may assume the following about this graph: the graph crosses the x-axis at (-3,0), (-1,0) and (1.5,0); and the graph has turning points at (-2,3) and (0.5,-3). Be sure to observe the scales carefully!

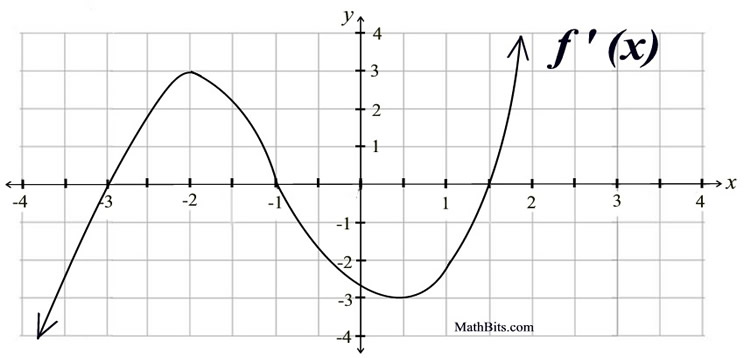1. What is the x-coordinate of a relative (local) maximum of f (x)?

2. Which choice shows intervals upon which f (x) is increasing?
1) (-4,-3) and (1.5,2)
2) (-3,-1) and (-1,1.5)
3) (-3,-1) and (1.5,2)
4) (-4,-3) and (1.5,2)
5) (-2,-1) and (-1,0.5)

3. At what postive x-coordinate will the graph of f " (x) cross the x-axis?

4. How many horizontal tangent lines can be drawn to f (x)?

5. Which choice shows an interval upon which f (x) is concave down?
1) (-4,-2)
2) (-3,-1)
3) (-2,0.5)
4) (-1,1.5)
5) (-4,-3)