
Exponential Regression Model Example
(when doing an exponential regression, the y-values must be greater than 0)

Exponential Regression Model Example
(when doing an exponential regression, the y-values must be greater than 0)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
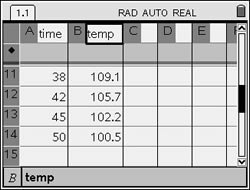
Step 1. Enter the data into the lists. Be sure to NAME the lists. For basic entry of data, see Lists & Spreadsheets. Resize the columns to see the names.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
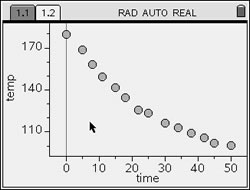
Step 2. Create a scatter plot of the data. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
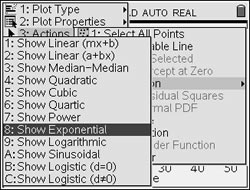
Step 3. Plot an Exponential Regression Model.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
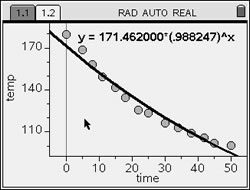
Step 4. The graph of the Exponential Regression model appears. Regression Equation: |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
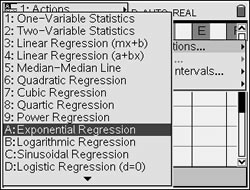
Step 5. Get statistical information. Press MENU - #4 Statistics - #1 Stat Calculations - #A Exponential Regression |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
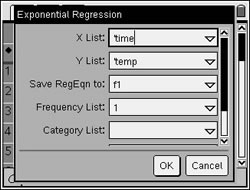
Step 6. Choose X list: time Choose Y list: temp Save RegEqn to: f1 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
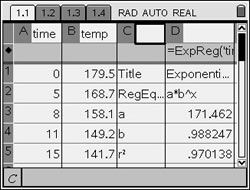
Step 7. The statistical information will appear in Columns C and D. If you arrow down you will see the r value and the Residuals.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Step 8. Is this model a "good fit"? The correlation coefficient, r, is -.984956 which places the correlation into the "strong" category. (0.8 or greater is a "strong" correlation) The coefficient of determination, r 2, is .970138 which means that 97% of the total variation in y can be explained by the relationship between x and y. Yes, it is a very "good fit". (answer to part c) |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Step 9. Based upon the new equation, what was the initial temperature of the coffee? The exponential regression equation is where x stands for time. The initial temperature would occur when the time equals zero. Substituting zero for x gives an initial temperature of 171.462º. (answer to part d) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
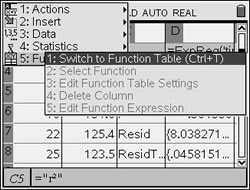
Step 10. Interpolate: (within the data set) |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
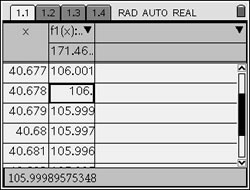
Look through the table to get an idea of approximately where the 106 temperature may occur. It is around a time of 40. To change the table settings to get a more accurate reading, choose MENU - #5 Function Table - #3 Edit Function Table Settings |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
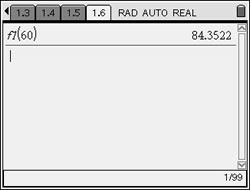
| Step 11. Extrapolate data: (beyond the data set) |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
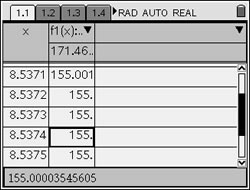
Step 12. How long should the restaurants wait (after pouring the coffee from the pot) before serving coffee, to ensure that the coffee is not hotter than 155º ?
Repeat procedure from Step 10. Go back to that page and reset the Function Table settings: (answer to part g -- approx. 8.5 minutes) |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Step 13. If the temperature in the room is 76° F, what will happen to the temperature of the coffee, after being poured from the pot, over an extended period of time?
The new exponential equation shows that the coffee will reach room temperature after 68.8 minutes. The exponential graph is asymptotic to the x-axis, therefore the y-values approach zero. This can be seen by observing successively larger values substituted into the new exponential equation (see Calculator screen screen substitutions at the right). Even though the graph approaches zero asymptotically, the temperature of the coffee will stop cooling once it reaches room temperature of 76º, and will not continue following the curve of the graph. (Also, remember that when extrapolating data, the further away from the data set you go, the less reliable your new data becomes.) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
Table of Contents | MathBits.com | Terms of Use