|

Complex Numbers
The graphing calculator can be a very
useful tool for checking your work with complex numbers.
Keep in mind, when working with a graphing
calculator,
that there may be more than one way
to arrive at an answer. |
Note: Complex numbers can be
accessed from Real Mode (without placing calculator in a + bi Mode).
Real mode, however, does not display complex results unless complex
numbers are entered as input. For example, if the calculator is NOT
in a + bi Mode, 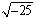 will create an error. will create an error. |
Now, let's look
at the arithmetic of complex
numbers:
Using the calculator to investigate powers of i:
|
Investigate
the powers of i. |
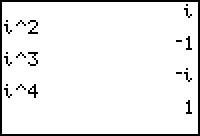 |
These values
will appear when you are in either
Real Mode or
in
a + bi mode. |
You can look at many powers at once by using a list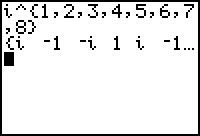
|
.. .
use right arrow to scroll to the right to see all of the answers
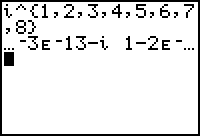 |

What kind of number is
- 3E - 13 - i???
This number is really just - i.
- 3E - 13 is so small, it is considered to be
zero.
(E-13 is Scientific Notation meaning 10 raised to -13
power.)
The older the calculator, the "sooner" you will start to see these scientific notation answers. |
The TI-84+CE is better with finding powers of i, but it, as well, will resort to the slightly less accurate scientific notation listings as the powers get larger. ------>
TI-84+CE is OK through a power of 100. |
|
|
"My Deer, BEWARE!!!
When raising i to a power on the graphing calculator, accuracy diminishes as the powers increase.
|
|
|
We know mathematically
that i178 is i2 which is -1.
On all of the TI-84+ family calculators,
i178 = -1+2.2E-12i.
But it is actually just -1.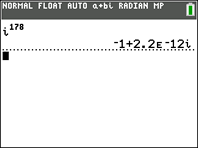
|
Special Calculator Functions for Complex Numbers:
There are also special functions on the
graphing calculator to deal with complex numbers
(but you probably won't
need a calculator for many of these functions):
Hit MATH key and arrow
to the right to CPX:
 |
1. conj( returns the complex conjugate of a complex number.
conj(2+5i)
gives 2-5i
2. real( returns the "a"
value in an a+bi complex number.
real(2+5i)
gives 2
3. imag( returns the "b"
value in an a+bi complex number.
imag(2+5i)
gives 5 |
|
4. angle( returns the angle, or argument, of the complex number - the angle formed by the positive x-axis (the positive real axis) and the segment from the origin to the complex number point on an Argand diagram.
angle(2+5i) gives 68.199º (with calculator set in degree mode)
5. abs( returns the absolute value (magnitude) of the complex number.
abs(5+12i) gives
13
abs (2 + 5i) gives 5.385164807
(Note: The absolute
value of a complex number may also be called its magnitude.
It you plot a complex number as a single point, the absolute value
represents the distance from the origin to that point. If you
plot a complex number as a vector, the absolute value represents the length of the vector.)
|
|