|

Conics: Graphing Hyperbolas
|
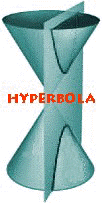
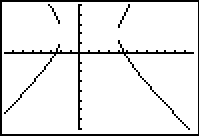
Example: Graph: 
|
 |
Solution:
- Solve the equation
for y.
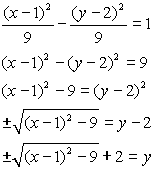
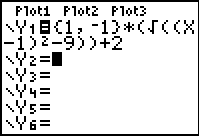
- Enter the equation with the positive square root into Y1.
- Enter the equation with the negative square root into Y2. You cannot simply negate Y1 to obtain
Y2 in this problem.
- OR enter using the {list} approach as shown at the right.
- If you choose ZOOM #6 (the standard
window), remember that the viewing window has a 3/2 aspect ratio (the standard
viewing screen is not a square).
- Choose ZOOM#5 ZSquare to create a
viewing window where the units on both axes are the same length.
- To see more of the graph, choose ZOOM #3
(Zoom Out).
|
|
NOTE:
* You may notice that
the "vertical" edges of the graph may not appear in the
viewing window. The viewing screen cannot graph points
that fall between pixels.
* You may notice that
the TRACE function will not move automatically between the
two sections of the graph because the positive and negative
square roots were graphed as two separate equations.
The arrow keys can be used to move between the two sections of
the graph. Also, the cursor will disappear if it is
moved beyond the domain for which x is defined. |

Finding
Your Way Around TABLE of CONTENTS
|