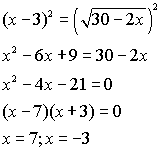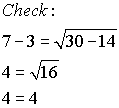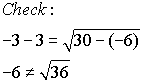|
Solving Radical Equations |
As you know, radical equations involving square roots are typically
solved by isolating a radical and squaring both sides of the resulting
equation. This process of squaring may lead to an answer that is
actually NOT one of the roots of the original equation. This "extra"
answer is called an extraneous root. The graphing
calculator is a wonderful back-up checking tool to determine if a root
is extraneous. Note the example below:
Example: Solve
the following equation algebraically and check.
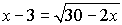
Algebraic Solution:
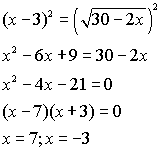
|
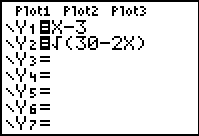
Graphical check:
Enter the left side of the equation into Y1.
Enter the right side of the equation into Y2.
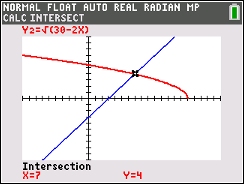
Use the INTERSECT option
(2nd Trace #5).
 |
x = 7
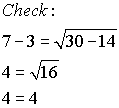 |
x = -3
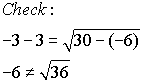
extraneous root |
The calculator clearly shows that there is only one solution (x
= 7), thus showing that x = -3 is an extraneous root.
 |
Algebraic Calculator CHECK:
Use your calculator to check your work, by storing each answer in x, and then letting the calculator determine if it is a solution to the equation.
The "store" command is activated by the sto→ key (on the lower left side of the calculator)
Store 7 in the variable x: 7 sto→ x. ENTER
Type the equation.
"=" sign (TEST (2nd MATH) #1), ENTER
"1" (true) means 7 is a solution.
Store -3 in variable x: -3 sto→ x. ENTER
Type the equation.
"0" (false) means -3 is NOT a solution. |
Have the calculator CHECK your work.

"1" stands for "true". It indicates that the stored value is a solution for the equation.
"0" stands for "false". It indicates that the stored value is NOT a solution for the equation. |
|
Hint: When working with
radical equations, it may be difficult to "see" the intersection point
if the viewing window is a small representation of the graph. You
may want to enlarge the viewing window by adjusting the
WINDOW settings or by using
ZOOM (#2 Zoom In). Remember, when
using Zoom In, hitting
ENTER the first time only registers the
function. You must hit ENTER a second
time to activate the Zoom In option.
You can quickly return to the 10 x 10 viewing window by pressing
ZOOM (#6 ZStandard).
Remember: In the example
above, you can see that there is only one answer to the equation since
there is only one point of intersection. Should there be NO points
of intersection, the answer will be the empty set.
|